
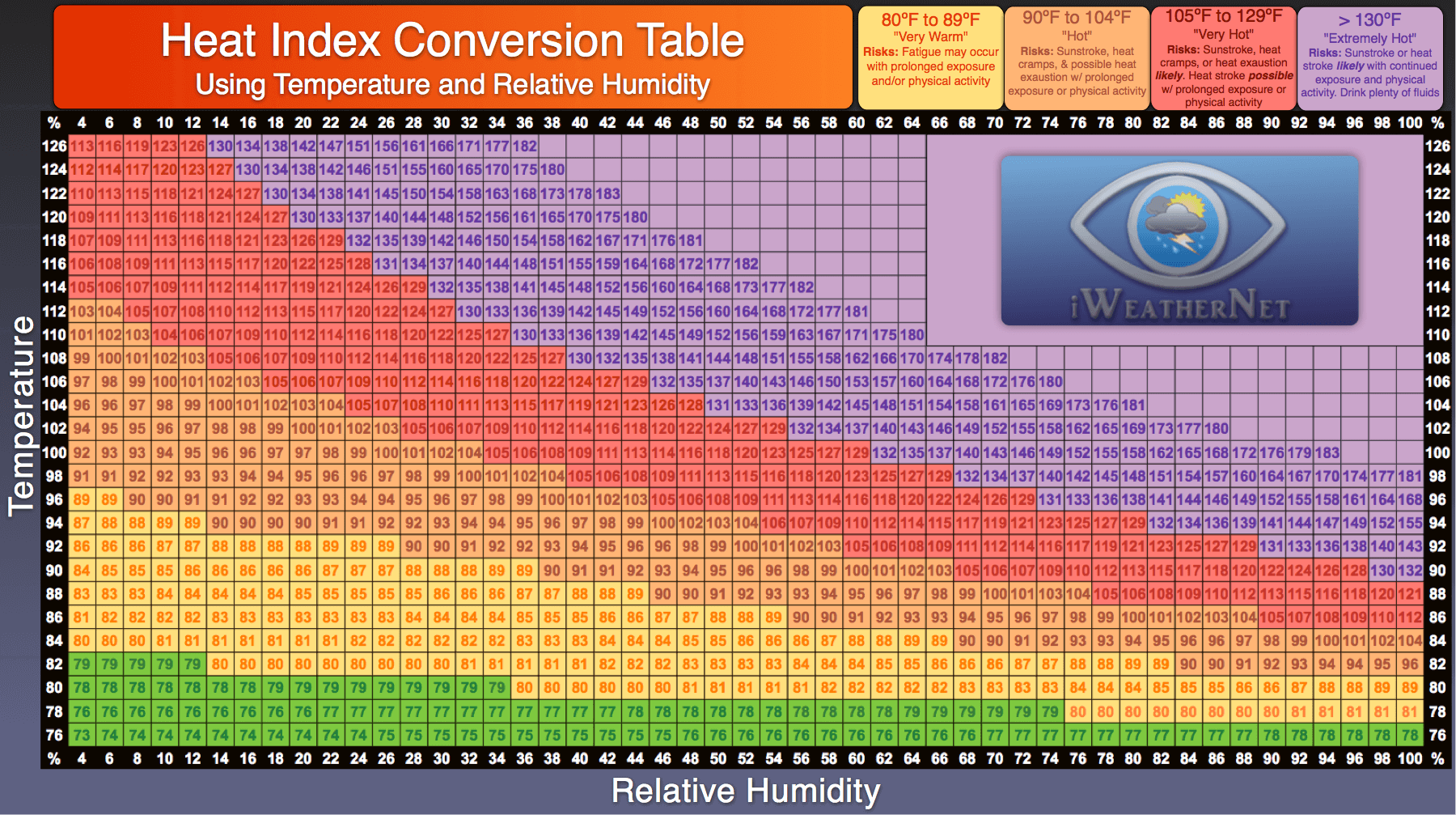

It killed more than 30,000 people as a result of exposure to extremely high temperatures coupled with a lack of widespread access to modern air conditioning in large parts of Europe. Let's start with the single example of the 2003 European heat wave. So, is there evidence that this is really happening? Indeed, there is. As we will see, a doubling of the probability of record heat extremes is not at all out of line with what we actually are seeing in the temperature observations. We now would expect twice as many days in July (2 per year) to exceed the century mark. That is nearly double the probability (2.5%) we calculated before the warming occurred. Using the online calculator, and taking z = 1.8 we get a one-sided probability of 3.6% for exceeding 100☏, i.e. Now, with the mean of 29☌ (and assuming the standard deviation is still 5☌), a 'century mark' temperature of 38☌/100☏ is only 1.8 s.d. We can represent the effect of this warming by shifting the entire temperature distribution to the right by 1☌ as shown qualitatively in the schematic above. Now, consider the effect of a hypothetical warming of 1☌/2☏ (the rough actual warming of the globe since pre-industrial time). Put in even more basic terms, we would only expect one day in July when the temperature would exceed the 'century mark' of 100☏. Only roughly 2.5% of the time would it be expected to exceed 2 s.d. Then, using what we know about the standard deviation, roughly 16% of the time, the daily high temperature would be expected to exceed 1 s.d. Let us consider a hypothetical city where the mean daily high temperature in July is 28☌ (82☏), and the standard deviation in that measure (i.e., the amplitude of typical day-to-day fluctuations) is 5☌ (9☏). Let's work out a simple example based on things we already know about the standard deviation.
Note from this schematic that even a modest warming can lead to a dramatic increase in the shaded region that exceeds some threshold (i.e., that exceeds 1 or even 2 standard deviations above the mean). Credit: IPCC 4th Assessment Report, Working Group 1 Report


 0 kommentar(er)
0 kommentar(er)
